マトリックス&ベクトルライブラリ ヘッダ More...
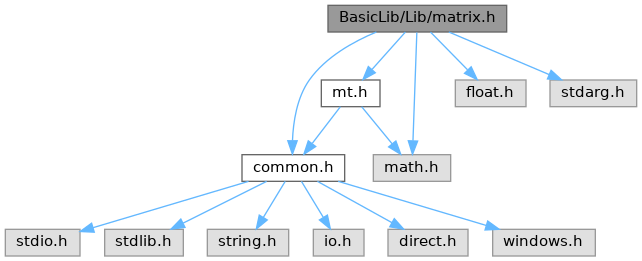
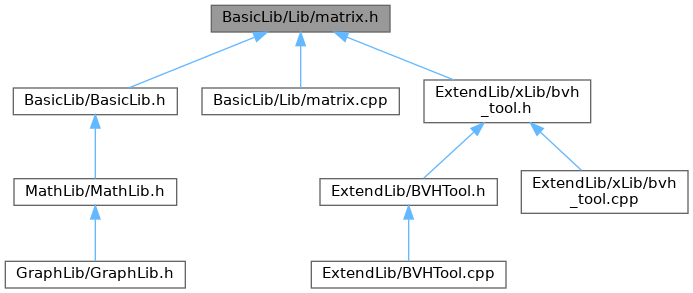
Go to the source code of this file.
Classes | |
| struct | ivector |
| struct | vector |
| struct | quaternion |
| struct | imatrix |
| struct | matrix |
Macros | |
| #define | in_vector(a, b) ((a).x*(b).x+(a).y*(b).y+(a).z*(b).z) |
| ベクトル a, bの内積をとる. | |
| #define | add_vector(a, b) set_vector((a).x+(b).x,(a).y+(b).y,(a).z+(b).z) |
| ベクトル a, bを足し算して, 結果を実数ベクトルで返す. | |
| #define | sub_vector(a, b) set_vector((a).x-(b).x,(a).y-(b).y,(a).z-(b).z) |
| ベクトル a, bを引き算して, 結果を実数ベクトルで返す. | |
| #define | add_ivector(a, b) set_ivector((a).x+(b).x,(a).y+(b).y,(a).z+(b).z) |
| ベクトル a, bを足し算して, 結果を整数ベクトルで返す. | |
| #define | sub_ivector(a, b) set_ivector((a).x-(b).x,(a).y-(b).y,(a).z-(b).z) |
| ベクトル a, bを引き算して, 結果を整数ベクトルで返す. | |
| #define | normal_vector(a) (a).r = sqrt((double)((a).x*(a).x)+(a).y*(a).y+(a).z*(a).z); |
| ベクトル aの大きさを計算する. | |
| #define | Vt(m, i) ((m).mx[(i)-1]) |
| 1次元マトリックスの i番目の要素を返す.1から数える. | |
| #define | Mx(m, i, j) ((m).mx[(j)-1+(m).sz[1]*((i)-1)]) |
| 2次元マトリックスの(i,j)要素を返す. 1から数える. | |
| #define | Mx1(m, i) ((m).mx[(i)-1]) |
| 1次元マトリックスの i番目の要素を返す.1から数える. | |
| #define | Mx2(m, i, j) ((m).mx[(j)-1+(m).sz[1]*((i)-1)]) |
| 2次元マトリックスの(i,j)要素を返す. 1から数える. | |
| #define | Mx3(m, i, j, k) ((m).mx[(k)-1+(m).sz[2]*((j)-1)+(m).sz[1]*(m).sz[2]*((i)-1)]) |
| 3次元マトリックスの(i,j,k)要素を返す. 1から数える. | |
| #define | Mx4(m, i, j, k, l) |
| 4次元マトリックスの(i,j,k,l)要素を返す.1から数える. | |
Detailed Description
Definition in file matrix.h.
Macro Definition Documentation
◆ add_ivector
| #define add_ivector | ( | a, | |
| b ) set_ivector((a).x+(b).x,(a).y+(b).y,(a).z+(b).z) |
◆ add_vector
| #define add_vector | ( | a, | |
| b ) set_vector((a).x+(b).x,(a).y+(b).y,(a).z+(b).z) |
◆ in_vector
| #define in_vector | ( | a, | |
| b ) ((a).x*(b).x+(a).y*(b).y+(a).z*(b).z) |
◆ Mx
| #define Mx | ( | m, | |
| i, | |||
| j ) ((m).mx[(j)-1+(m).sz[1]*((i)-1)]) |
Definition at line 84 of file matrix.h.
Referenced by decompQR(), and invrU_matrix().
◆ Mx1
◆ Mx2
◆ Mx3
| #define Mx3 | ( | m, | |
| i, | |||
| j, | |||
| k ) ((m).mx[(k)-1+(m).sz[2]*((j)-1)+(m).sz[1]*(m).sz[2]*((i)-1)]) |
◆ Mx4
| #define Mx4 | ( | m, | |
| i, | |||
| j, | |||
| k, | |||
| l ) |
◆ normal_vector
| #define normal_vector | ( | a | ) | (a).r = sqrt((double)((a).x*(a).x)+(a).y*(a).y+(a).z*(a).z); |
◆ sub_ivector
| #define sub_ivector | ( | a, | |
| b ) set_ivector((a).x-(b).x,(a).y-(b).y,(a).z-(b).z) |
◆ sub_vector
| #define sub_vector | ( | a, | |
| b ) set_vector((a).x-(b).x,(a).y-(b).y,(a).z-(b).z) |
◆ Vt
| #define Vt | ( | m, | |
| i ) ((m).mx[(i)-1]) |
Definition at line 83 of file matrix.h.
Referenced by decompQR().
Function Documentation
◆ add_imatrix()
imatrix add_imatrix(imatrix a, imatrix b)
マトリックスの足し算. 整数マトリックス a, bを足し算して,結果の整数マトリックスを返す.
- Parameters
-
a 足されるマトリックス. b 足すマトリックス.
- Returns
- 足し算結果の整数マトリックス.
Definition at line 594 of file matrix.cpp.
References make_imatrix(), imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.

◆ add_matrix()
matrix add_matrix(matrix a, matrix b)
マトリックスの足し算. 実数マトリックス a, bを足し算して,結果の実数マトリックスを返す.
- Parameters
-
a 足されるマトリックス. b 足すマトリックス.
- Returns
- 足し算結果のマトリックス.
Definition at line 567 of file matrix.cpp.
References make_matrix(), matrix::mx, matrix::n, matrix::r, and matrix::sz.

◆ clear_imatrix()
| void clear_imatrix | ( | imatrix * | a | ) |
◆ clear_matrix()
| void clear_matrix | ( | matrix * | a | ) |
◆ copy_imatrix()
void copy_imatrix(imatrix src, imatrix dst)
整数マトリックスのコピー.srcの内容を dstへコピーする.
マトリックス全体のサイズが合わない場合は何もしない.
全体のサイズが合っていればコピーする.
- Parameters
-
src コピー元マトリックス. dst コピー先マトリックス.
Definition at line 545 of file matrix.cpp.
References imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.
◆ copy_matrix()
void copy_matrix(matrix src, matrix dst)
マトリックスのコピー.srcの内容を dstへコピーする.
マトリックス全体のサイズが合わない場合は何もしない.
全体のサイズが合っていればコピーする.
- Parameters
-
src コピー元マトリックス. dst コピー先マトリックス.
Definition at line 523 of file matrix.cpp.
References matrix::mx, matrix::n, matrix::r, and matrix::sz.
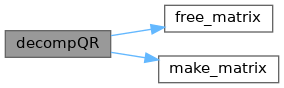
◆ decompQR()
matrix decompQR(matrix xx, imatrix col)
2次元行列 xxのQR分解を行い,R行列を返す.
xx = Q・R
- xxのQR分解を行った後,係数のマトリックス(上三角行列 R)を返す.
- ピボット操作(列の入れ換え)をした場合は整数ベクトル colに Qの 基底ベクトルが入る.
- colは予め make_imatrix()等によって確保されていなければならない.
- Parameters
-
xx QR分解を行う2次元行列. col メモリを確保し,初期化しておく.Qの基底ベクトルが入る.
- Returns
- 上三角行列 R
Definition at line 869 of file matrix.cpp.
References free_matrix(), make_matrix(), imatrix::mx, matrix::mx, Mx, matrix::n, matrix::r, imatrix::sz, matrix::sz, and Vt.
Referenced by minimum2().

◆ ex_vector()
vector ex_vector(vector a, vector b)
ベクトルの外積. 実数ベクトル a,b の外積ベクトルを計算し,それを返す.
- Parameters
-
a 外積を計算するベクトル. b 外積を計算するベクトル.
- Returns
- 外積ベクトル.
Definition at line 167 of file matrix.cpp.
◆ f2ivector()
ivector f2ivector(vector a)
実数ベクトル a から整数ベクトルをつくり出し,それを返す. 各要素は四捨五入される.
- Parameters
-
a 変換する実数ベクトル.
- Returns
- 変換された整数ベクトル.
Definition at line 125 of file matrix.cpp.
References ivector::n, ivector::x, vector::x, ivector::y, vector::y, ivector::z, and vector::z.
◆ free_imatrix()
| void free_imatrix | ( | imatrix * | a | ) |
整数マトリックスのバッファ部を開放する.
- Parameters
-
a 開放するバッファ部を持った整数マトリックスへのポインタ.
Definition at line 425 of file matrix.cpp.
References imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.
Referenced by minimum2().

◆ free_matrix()
| void free_matrix | ( | matrix * | a | ) |
マトリックスのバッファ部を開放をする.
- Parameters
-
a 開放するバッファ部を持ったマトリックスへのポインタ.
Definition at line 408 of file matrix.cpp.
References matrix::mx, matrix::n, matrix::r, and matrix::sz.
Referenced by decompQR(), and minimum2().

◆ get_imatrix()
| int * get_imatrix | ( | imatrix | mtx, |
| ... ) |
int* get_imatrix(imatrix mtx, ...)
Matrix の要素を返す.次元数に制限はない.インデックスは1から数える(0からではない).
Definition at line 488 of file matrix.cpp.
References imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.
◆ get_matrix()
| double * get_matrix | ( | matrix | mtx, |
| ... ) |
double* get_matrix(matrix mtx, ...)
Matrix の要素を返す.次元数に制限はない.インデックスは1から数える(0からではない).
Definition at line 449 of file matrix.cpp.
References matrix::mx, matrix::n, matrix::r, and matrix::sz.
◆ i2vector()
vector i2vector(ivector a)
整数ベクトル a から実数ベクトルをつくり出し,それを返す.
- Parameters
-
a 変換する整数ベクトル.
- Returns
- 変換された実数ベクトル.
Definition at line 145 of file matrix.cpp.
References vector::n, ivector::x, vector::x, ivector::y, vector::y, ivector::z, and vector::z.
◆ invrU_matrix()
matrix invrU_matrix(matrix x)
2次元の上三角行列 xの逆行列を求める.
- Parameters
-
x 操作対象行列(上三角行列).
- Returns
- xの逆行列.
Definition at line 1045 of file matrix.cpp.
References make_matrix(), matrix::mx, Mx, matrix::n, matrix::r, and matrix::sz.
Referenced by minimum2().


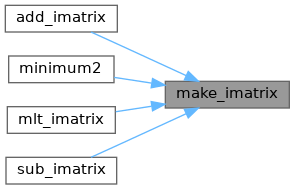
◆ make_imatrix()
| imatrix make_imatrix | ( | int | n, |
| int * | sz ) |
imatrix make_imatrix(int n, int* sz)
任意(n)次元の整数マトリックスのバッファ部をつくり出す. 要素自体は 0に初期化される.
- Parameters
-
n マトリックスの次元数. sz sz[0]〜sz[n-1]: 各次元の要素数.
- Returns
- 作成された整数マトリックス.
Definition at line 371 of file matrix.cpp.
References imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.
Referenced by add_imatrix(), minimum2(), mlt_imatrix(), and sub_imatrix().
◆ make_imatrix1()
| imatrix make_imatrix1 | ( | int | n | ) |
imatrix make_imatrix1(int n)
1次元の整数行列のバッファ部をつくり出す. 要素自体は 0に初期化される.
- Parameters
-
n 1次元行列の大きさ.
- Returns
- 作成された1次元整数行列
Definition at line 222 of file matrix.cpp.
References imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.
◆ make_imatrix2()
| imatrix make_imatrix2 | ( | int | n, |
| int | m ) |
imatrix make_imatrix2(int n, int m)
2次元の整数行列のバッファ部をつくり出す. 要素自体は 0に初期化される.
- Parameters
-
n 2次元行列の行の数. m 2次元行列の列の数.
- Returns
- 作成された2次元整数行列
Definition at line 294 of file matrix.cpp.
References imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.
◆ make_matrix()
| matrix make_matrix | ( | int | n, |
| int * | sz ) |
matrix make_matrix(int n, int* sz)
任意(n)次元の実数マトリックスのバッファ部をつくり出す. 要素自体は 0.0に初期化される.
- Parameters
-
n マトリックスの次元数. sz sz[0]〜sz[n-1]: 各次元の要素数.
- Returns
- 作成されたマトリックス.
Definition at line 331 of file matrix.cpp.
References matrix::mx, matrix::n, matrix::r, and matrix::sz.
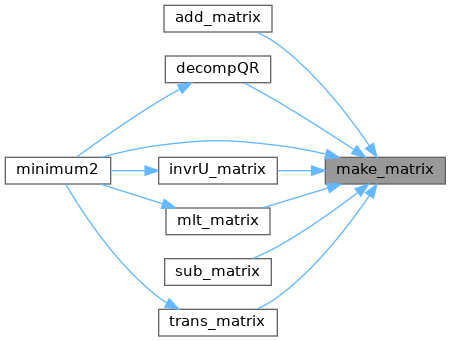
Referenced by add_matrix(), decompQR(), invrU_matrix(), minimum2(), mlt_matrix(), sub_matrix(), and trans_matrix().
◆ make_matrix1()
| matrix make_matrix1 | ( | int | n | ) |
matrix make_matrix1(int n)
1次元の実数行列のバッファ部をつくり出す. 要素自体は 0.0に初期化される.
- Parameters
-
n 1次元行列の大きさ.
- Returns
- 作成された1次元行列
Definition at line 188 of file matrix.cpp.
References matrix::mx, matrix::n, matrix::r, and matrix::sz.
◆ make_matrix2()
| matrix make_matrix2 | ( | int | n, |
| int | m ) |
matrix make_matrix2(int n, int m)
2次元の実数行列のバッファ部をつくり出す. 要素自体は 0.0に初期化される.
- Parameters
-
n 2次元行列の行の数. m 2次元行列の列の数.
- Returns
- 作成された2次元行列
Definition at line 257 of file matrix.cpp.
References matrix::mx, matrix::n, matrix::r, and matrix::sz.
◆ minimum2()
matrix minimum2(matrix y, matrix x)
最小2乗法で方程式の近似解を解き,結果を返す. ただし, x,yは2次元行列のみ.
- Parameters
-
y 連立方程式の結果の行列 (例を見よ) x 連立方程式の変数の行列 (例を見よ)
- Returns
- 連立方程式の係数の行列 (例を見よ)
- 例
- 以下の場合 A = minimum2(Y, X) で解く(a1,a2を求める). Y = X・Ay1 = x11*a1 + x12*a2y2 = x21*a1 + x22*a2y3 = x31*a1 + x32*a2
Definition at line 967 of file matrix.cpp.
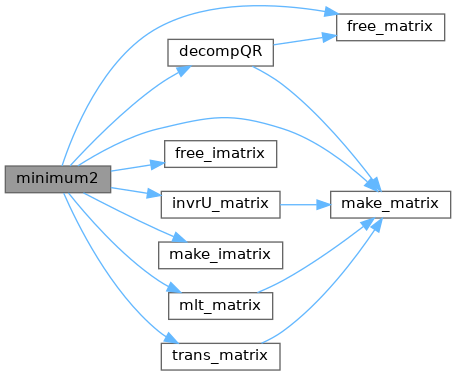
References decompQR(), free_imatrix(), free_matrix(), invrU_matrix(), make_imatrix(), make_matrix(), mlt_matrix(), imatrix::mx, matrix::mx, matrix::n, matrix::r, matrix::sz, and trans_matrix().
◆ mlt_imatrix()
imatrix mlt_imatrix(imatrix a, imatrix b)
マトリックスのかけ算. 整数マトリックス a, bをかけ算して,結果の整数マトリックスを返す.
- Parameters
-
a かけられるマトリックス. b かけるマトリックス.
- Returns
- かけ算結果の整数マトリックス.
Definition at line 751 of file matrix.cpp.
References make_imatrix(), imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.

◆ mlt_matrix()
matrix mlt_matrix(matrix a, matrix b)
マトリックスのかけ算. 実数マトリックス a, bをかけ算して,結果の実数マトリックスを返す.
- Parameters
-
a かけられるマトリックス. b かけるマトリックス.
- Returns
- かけ算結果のマトリックス.
Definition at line 675 of file matrix.cpp.
References make_matrix(), matrix::mx, matrix::n, matrix::r, and matrix::sz.
Referenced by minimum2().


◆ print_imatrix()
| void print_imatrix | ( | FILE * | fp, |
| imatrix | a ) |
void print_imatrix(FILE* fp, imatrix a)
整数マトリックスの要素を標準出力に書き出す.
- Parameters
-
fp 出力先のファイル記述子 a プリントするマトリックス.
Definition at line 843 of file matrix.cpp.
References imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.
◆ print_matrix()
| void print_matrix | ( | FILE * | fp, |
| matrix | a ) |
void print_matrix(FILE* fp, matrix a)
実数マトリックスの要素を標準出力に書き出す.
- Parameters
-
fp 出力先のファイル記述子 a プリントするマトリックス.
Definition at line 824 of file matrix.cpp.
References matrix::mx, matrix::n, matrix::r, and matrix::sz.
◆ set_ivector()
| ivector set_ivector | ( | int | x, |
| int | y, | ||
| int | z ) |
ivector set_ivector(int x, int y, int z)
整数ベクトルの作成.x方向成分, y方向成分, z方向成分から整数ベクトルを作り,それを返す.
- Parameters
-
x ベクトルの x成分. y ベクトルの y成分. z ベクトルの z成分.
- Returns
- 作成された整数ベクトル.
Definition at line 104 of file matrix.cpp.
References ivector::n, ivector::x, ivector::y, and ivector::z.
◆ set_vector()
| vector set_vector | ( | double | x, |
| double | y, | ||
| double | z ) |
vector set_vector(double x, double y, double z)
ベクトルの作成.x方向成分, y方向成分, z方向成分から実数ベクトルを作り,それを返す.
- Parameters
-
x ベクトルの x成分. y ベクトルの y成分. z ベクトルの z成分.
- Returns
- 作成されたベクトル.
Definition at line 82 of file matrix.cpp.
◆ sub_imatrix()
imatrix sub_imatrix(imatrix a, imatrix b)
マトリックスの引き算. 整数マトリックス a, bを引き算して,結果の整数マトリックスを返す.
- Parameters
-
a 引かれるマトリックス. b 引くマトリックス.
- Returns
- 引き算結果の整数マトリックス.
Definition at line 648 of file matrix.cpp.
References make_imatrix(), imatrix::mx, imatrix::n, imatrix::r, and imatrix::sz.

◆ sub_matrix()
matrix sub_matrix(matrix a, matrix b)
マトリックスの引き算. 実数マトリックス a, bを引き算して,結果の実数マトリックスを返す.
- Parameters
-
a 引かれるマトリックス. b 引くマトリックス.
- Returns
- 引き算結果のマトリックス.
Definition at line 621 of file matrix.cpp.
References make_matrix(), matrix::mx, matrix::n, matrix::r, and matrix::sz.

◆ trans_matrix()
matrix trans_matrix(matrix a)
2次元行列 aの転置行列を返す.
- Parameters
-
a 操作対象行列.
- Returns
- aの転置行列.
Definition at line 1013 of file matrix.cpp.
References make_matrix(), matrix::mx, matrix::n, matrix::r, and matrix::sz.
Referenced by minimum2().


◆ unit_ivector()
vector unit_ivector(ivector a)
整数ベクトル aの単位ベクトルを返す.返されるベクトルは実数ベクトル.
- Parameters
-
a 対象整数ベクトル.
- Returns
- a の単位ベクトル(実数ベクトル).
Definition at line 49 of file matrix.cpp.
References EPS, vector::n, ivector::x, vector::x, Xabs, ivector::y, vector::y, ivector::z, and vector::z.
◆ unit_vector()
vector unit_vector(vector a)
ベクトル aの単位ベクトルを返す.
- Parameters
-
a 対象ベクトル.
- Returns
- a の単位ベクトル.
Definition at line 18 of file matrix.cpp.
References EPS, vector::n, vector::x, Xabs, vector::y, and vector::z.