#include <Rotation.h>

Public Member Functions
	Quaternion (void)

	Quaternion (T S, T X, T Y, T Z, T N=(T) 0.0, T C=(T) 1.0)

	Quaternion (T S, Vector< T > v)

virtual	~Quaternion (void)

T	norm (void)

void	normalize (void)

void	set (T S, T X, T Y, T Z, T N=(T) 0.0, T C=(T) 1.0)

void	init (T C=(T) 1.0)

Vector< T >	getVector ()

T	getScalar ()

T	getAngle ()
	0〜2π

T	getMathAngle ()
	-π〜π

Matrix< T >	getRotMatrix ()

void	setRotation (T e, Vector< T > v)

void	setRotation (T e, T X, T Y, T Z, T N=(T) 0.0)

void	setRotate (T e, Vector< T > v)

void	setRotate (T e, T X, T Y, T Z, T N=(T) 0.0)

void	setExtEulerXYZ (Vector< T > e)
	X->Y->Z.

void	setExtEulerZYX (Vector< T > e)
	Z->Y->X.

void	setExtEulerXZY (Vector< T > e)
	X->Z->Y.

void	setExtEulerYZX (Vector< T > e)
	Y->Z->X.

void	setExtEulerYXZ (Vector< T > e)
	Y->X->Z.

void	setExtEulerZXY (Vector< T > e)
	Z->X->Y.

Vector< T >	getExtEulerXYZ (Vector< T > *vt=NULL)

Vector< T >	getExtEulerZYX (Vector< T > *vt=NULL)

Vector< T >	getExtEulerXZY (Vector< T > *vt=NULL)

Vector< T >	getExtEulerYZX (Vector< T > *vt=NULL)

Vector< T >	getExtEulerYXZ (Vector< T > *vt=NULL)

Vector< T >	getExtEulerZXY (Vector< T > *vt=NULL)

Vector< T >	execRotation (Vector< T > v)
	Exec Rotation qv(~q)

Vector< T >	execInvRotation (Vector< T > v)
	Exec Inv Rotation (~q)vq.

Vector< T >	execRotate (Vector< T > v)

Vector< T >	execInvRotate (Vector< T > v)

Public Attributes
T	s
	cos(θ/2)

T	x
	x 成分

T	y
	y 成分

T	z
	z 成分

T	n
	ノルム

T	c
	信頼度

Detailed Description

template<typename T = double>
class jbxl::Quaternion< T >

class DllExport Quaternion

クォータニオンの定義

回転の合成：A*B => Bの回転 -> Aの回転

Definition at line 43 of file Rotation.h.

Constructor & Destructor Documentation

◆ Quaternion() [1/3]

template<typename T = double>

Quaternion ( void )

inline

Definition at line 55 of file Rotation.h.

55{ init();}

jbxl::Quaternion::init

void init(T C=(T) 1.0)

Definition Rotation.h:64

◆ Quaternion() [2/3]

template<typename T = double>

Quaternion	(	T	S,
		T	X,
		T	Y,
		T	Z,
		T	N = (T)0.0,
		T	C = (T)1.0 )

inline

Definition at line 56 of file Rotation.h.

56{ set(S, X, Y, Z, N, C);}

jbxl::Quaternion::set

void set(T S, T X, T Y, T Z, T N=(T) 0.0, T C=(T) 1.0)

Definition Rotation.h:273

◆ Quaternion() [3/3]

template<typename T = double>

Quaternion	(	T	S,
		Vector< T >	v )

inline

Definition at line 57 of file Rotation.h.

57{ setRotation(S, v);}

jbxl::Quaternion::setRotation

void setRotation(T e, Vector< T > v)

Definition Rotation.h:311

◆ ~Quaternion()

template<typename T = double>

virtual ~Quaternion ( void )

inlinevirtual

Definition at line 58 of file Rotation.h.

58{}

Member Function Documentation

◆ execInvRotate()

template<typename T = double>

Vector< T > execInvRotate ( Vector< T > v )

inline

Definition at line 97 of file Rotation.h.

97{ return execInvRotation(v);}

jbxl::Quaternion::execInvRotation

Vector< T > execInvRotation(Vector< T > v)

Exec Inv Rotation (~q)vq.

Definition Rotation.h:480

◆ execInvRotation()

template<typename T >

Vector< T > execInvRotation ( Vector< T > v )

Definition at line 480 of file Rotation.h.

{
    if (c<(T)0.0) return v;
 
    Quaternion<T> inv = ~(*this);
    Quaternion<T> qut =  inv*(v*(*this));
    Vector<T> vct = qut.getVector();
    vct.d = v.d;
 
    return vct;
}

References Vector< T >::d, and Quaternion< T >::getVector().

Here is the call graph for this function:

◆ execRotate()

template<typename T = double>

Vector< T > execRotate ( Vector< T > v )

inline

Definition at line 96 of file Rotation.h.

96{ return execRotation(v);}

jbxl::Quaternion::execRotation

Vector< T > execRotation(Vector< T > v)

Exec Rotation qv(~q)

Definition Rotation.h:466

◆ execRotation()

template<typename T >

Vector< T > execRotation ( Vector< T > v )

Definition at line 466 of file Rotation.h.

{
    if (c<(T)0.0) return v;
 
    Quaternion<T> inv = ~(*this);
    Quaternion<T> qut =  (*this)*(v*inv);
    Vector<T> vct = qut.getVector();
    vct.d = v.d;
 
    return vct;
}

References Vector< T >::d, and Quaternion< T >::getVector().

Referenced by ContourTriData::execRotate().

Here is the call graph for this function:

Here is the caller graph for this function:

◆ getAngle()

template<typename T = double>

T getAngle ( )

inline

Definition at line 68 of file Rotation.h.

◆ getExtEulerXYZ()

template<typename T = double>

Vector< T > getExtEulerXYZ ( Vector< T > * vt = NULL )

inline

Definition at line 87 of file Rotation.h.

87{ return Quaternion2ExtEulerXYZ<T>(*this, vt);}

◆ getExtEulerXZY()

template<typename T = double>

Vector< T > getExtEulerXZY ( Vector< T > * vt = NULL )

inline

Definition at line 89 of file Rotation.h.

89{ return Quaternion2ExtEulerXZY<T>(*this, vt);}

◆ getExtEulerYXZ()

template<typename T = double>

Vector< T > getExtEulerYXZ ( Vector< T > * vt = NULL )

inline

Definition at line 91 of file Rotation.h.

91{ return Quaternion2ExtEulerYXZ<T>(*this, vt);}

◆ getExtEulerYZX()

template<typename T = double>

Vector< T > getExtEulerYZX ( Vector< T > * vt = NULL )

inline

Definition at line 90 of file Rotation.h.

90{ return Quaternion2ExtEulerYZX<T>(*this, vt);}

◆ getExtEulerZXY()

template<typename T = double>

Vector< T > getExtEulerZXY ( Vector< T > * vt = NULL )

inline

Definition at line 92 of file Rotation.h.

92{ return Quaternion2ExtEulerZXY<T>(*this, vt);}

◆ getExtEulerZYX()

template<typename T = double>

Vector< T > getExtEulerZYX ( Vector< T > * vt = NULL )

inline

Definition at line 88 of file Rotation.h.

88{ return Quaternion2ExtEulerZYX<T>(*this, vt);}

◆ getMathAngle()

template<typename T = double>

T getMathAngle ( )

inline

Definition at line 69 of file Rotation.h.

References PI, and PI2.

Referenced by jbxl::SlerpQuaternion().

Here is the caller graph for this function:

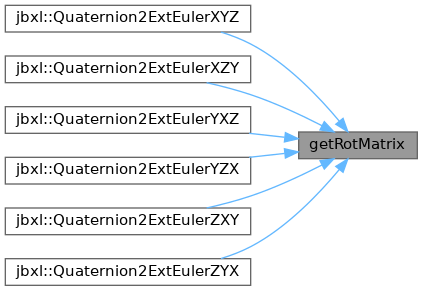
◆ getRotMatrix()

template<typename T >

Matrix< T > getRotMatrix ( )

ベクトルを回転させる場合の回転行列を求める．座標軸の回転の場合は共役クォータニオンで計算する．

Definition at line 445 of file Rotation.h.

{
    Matrix<T> mtx(2, 3, 3);    // 2次元マトリックス, 3x3
 
    if (n!=(T)1.0) normalize();
 
    mtx.element(1, 1) = (T)1.0 - (T)2.0*y*y - (T)2.0*z*z;
    mtx.element(1, 2) = (T)2.0*x*y - (T)2.0*s*z;
    mtx.element(1, 3) = (T)2.0*x*z + (T)2.0*s*y;
    mtx.element(2, 1) = (T)2.0*x*y + (T)2.0*s*z;
    mtx.element(2, 2) = (T)1.0 - (T)2.0*x*x - (T)2.0*z*z;
    mtx.element(2, 3) = (T)2.0*y*z - (T)2.0*s*x;
    mtx.element(3, 1) = (T)2.0*x*z - (T)2.0*s*y;
    mtx.element(3, 2) = (T)2.0*y*z + (T)2.0*s*x;
    mtx.element(3, 3) = (T)1.0 - (T)2.0*x*x - (T)2.0*y*y;
 
    return mtx;
}

References Matrix< T >::element().

Referenced by jbxl::Quaternion2ExtEulerXYZ(), jbxl::Quaternion2ExtEulerXZY(), jbxl::Quaternion2ExtEulerYXZ(), jbxl::Quaternion2ExtEulerYZX(), jbxl::Quaternion2ExtEulerZXY(), and jbxl::Quaternion2ExtEulerZYX().

Here is the call graph for this function:

Here is the caller graph for this function:

◆ getScalar()

template<typename T = double>

T getScalar ( )

inline

Definition at line 67 of file Rotation.h.

67{ return s;}

◆ getVector()

template<typename T = double>

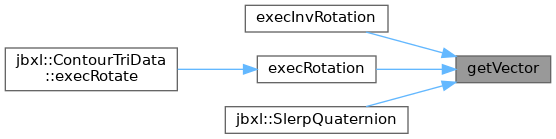
Vector< T > getVector ( )

inline

Definition at line 66 of file Rotation.h.

66{ Vector<T> v(x, y, z, (T)0.0, c); return v;}

Referenced by Quaternion< T >::execInvRotation(), Quaternion< T >::execRotation(), and jbxl::SlerpQuaternion().

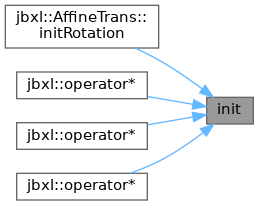
Here is the caller graph for this function:

◆ init()

template<typename T = double>

void init ( T C = (T)1.0 )

inline

Definition at line 64 of file Rotation.h.

64{ s=n=(T)1.0; x=y=z=(T)0.0; c=C;}

Referenced by AffineTrans< T >::initRotation(), jbxl::operator*(), jbxl::operator*(), and jbxl::operator*().

Here is the caller graph for this function:

◆ norm()

template<typename T = double>

T norm ( void )

inline

Definition at line 60 of file Rotation.h.

60{ n = (T)sqrt(s*s+x*x+y*y+z*z); return n;}

◆ normalize()

template<typename T >

void normalize ( void )

Definition at line 288 of file Rotation.h.

{
    T nrm = (T)sqrt(s*s + x*x + y*y + z*z);
    
    if (nrm>=Zero_Eps) {
        s  = s/nrm;
        x  = x/nrm;
        y  = y/nrm;
        z  = z/nrm;
        n  = (T)1.0;
    }
    else {
        init();
    }
}

References jbxl::Zero_Eps.

Referenced by jbxl::SlerpQuaternion().

Here is the caller graph for this function:

◆ set()

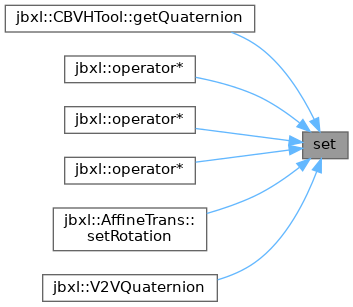
template<typename T >

void set	(	T	S,
		T	X,
		T	Y,
		T	Z,
		T	N = (T)0.0,
		T	C = (T)1.0 )

Definition at line 273 of file Rotation.h.

{
    s  = S;
    x  = X;
    y  = Y;
    z  = Z;
    n  = N;
    c  = C;
 
    if (n<=0.0) {
        n = (T)sqrt(s*s + x*x + y*y + z*z);
    }
}

Referenced by CBVHTool::getQuaternion(), jbxl::operator*(), jbxl::operator*(), jbxl::operator*(), AffineTrans< T >::setRotation(), and jbxl::V2VQuaternion().

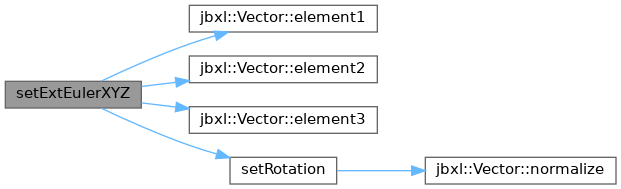
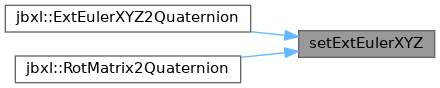
Here is the caller graph for this function:

◆ setExtEulerXYZ()

template<typename T >

void setExtEulerXYZ ( Vector< T > e )

Definition at line 356 of file Rotation.h.

{
    Vector<T> ex((T)1.0, (T)0.0, (T)0.0, (T)1.0);  
    Vector<T> ey((T)0.0, (T)1.0, (T)0.0, (T)1.0);  
    Vector<T> ez((T)0.0, (T)0.0, (T)1.0, (T)1.0);
 
    Quaternion<T> qx, qy, qz;
    qx.setRotation(e.element1(), ex);
    qy.setRotation(e.element2(), ey);
    qz.setRotation(e.element3(), ez);
 
    (*this) = qz*qy*qx;
    if (s<(T)0.0) (*this) = - (*this);
}

References Vector< T >::element1(), Vector< T >::element2(), Vector< T >::element3(), and Quaternion< T >::setRotation().

Referenced by jbxl::ExtEulerXYZ2Quaternion(), and jbxl::RotMatrix2Quaternion().

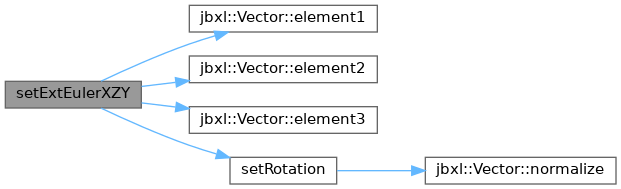
Here is the call graph for this function:

Here is the caller graph for this function:

◆ setExtEulerXZY()

template<typename T >

void setExtEulerXZY ( Vector< T > e )

Definition at line 390 of file Rotation.h.

{
    Vector<T> ex((T)1.0, (T)0.0, (T)0.0, (T)1.0);  
    Vector<T> ey((T)0.0, (T)1.0, (T)0.0, (T)1.0);  
    Vector<T> ez((T)0.0, (T)0.0, (T)1.0, (T)1.0);
 
    Quaternion<T> qx, qy, qz;
    qx.setRotation(e.element1(), ex);
    qz.setRotation(e.element2(), ez);
    qy.setRotation(e.element3(), ey);
 
    (*this) = qy*qz*qx;
    if (s<(T)0.0) (*this) = - (*this);
}

References Vector< T >::element1(), Vector< T >::element2(), Vector< T >::element3(), and Quaternion< T >::setRotation().

Referenced by jbxl::ExtEulerXZY2Quaternion().

Here is the call graph for this function:

Here is the caller graph for this function:

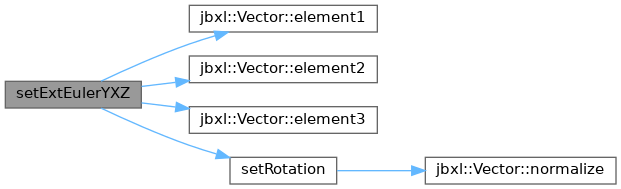
◆ setExtEulerYXZ()

template<typename T >

void setExtEulerYXZ ( Vector< T > e )

Definition at line 407 of file Rotation.h.

{
    Vector<T> ex((T)1.0, (T)0.0, (T)0.0, (T)1.0);  
    Vector<T> ey((T)0.0, (T)1.0, (T)0.0, (T)1.0);  
    Vector<T> ez((T)0.0, (T)0.0, (T)1.0, (T)1.0);
 
    Quaternion<T> qx, qy, qz;
    qy.setRotation(e.element1(), ey);
    qx.setRotation(e.element2(), ex);
    qz.setRotation(e.element3(), ez);
 
    (*this) = qz*qx*qy;
    if (s<(T)0.0) (*this) = - (*this);
}

References Vector< T >::element1(), Vector< T >::element2(), Vector< T >::element3(), and Quaternion< T >::setRotation().

Referenced by jbxl::ExtEulerYXZ2Quaternion().

Here is the call graph for this function:

Here is the caller graph for this function:

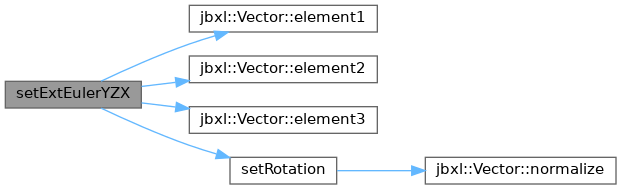
◆ setExtEulerYZX()

template<typename T >

void setExtEulerYZX ( Vector< T > e )

template <typename T> void Quaternion<T>::setExtEulerYZX(Vector<T> e)

Y->Z->X の順にオイラー角でベクトルを回転させる場合のクオータニオンを計算する．

Parameters

e	オイラー角の成分．作用させる順番に格納する．この場合, e.xはY軸回転，e.yはZ軸回転，e.z はX軸回転のそれぞれの回転角（ラジアン）を格納する．

Definition at line 339 of file Rotation.h.

{
    Vector<T> ex((T)1.0, (T)0.0, (T)0.0, (T)1.0);  
    Vector<T> ey((T)0.0, (T)1.0, (T)0.0, (T)1.0);  
    Vector<T> ez((T)0.0, (T)0.0, (T)1.0, (T)1.0);
 
    Quaternion<T> qx, qy, qz;
    qy.setRotation(e.element1(), ey);
    qz.setRotation(e.element2(), ez);
    qx.setRotation(e.element3(), ex);
 
    (*this) = qx*qz*qy;
    if (s<(T)0.0) (*this) = - (*this);
}

References Vector< T >::element1(), Vector< T >::element2(), Vector< T >::element3(), and Quaternion< T >::setRotation().

Referenced by jbxl::ExtEulerYZX2Quaternion().

Here is the call graph for this function:

Here is the caller graph for this function:

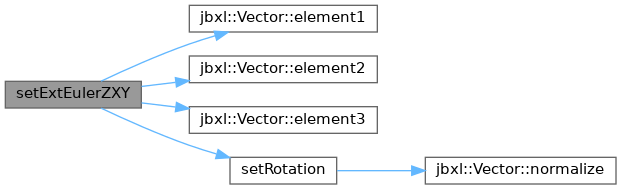
◆ setExtEulerZXY()

template<typename T >

void setExtEulerZXY ( Vector< T > e )

Definition at line 424 of file Rotation.h.

{
    Vector<T> ex((T)1.0, (T)0.0, (T)0.0, (T)1.0);  
    Vector<T> ey((T)0.0, (T)1.0, (T)0.0, (T)1.0);  
    Vector<T> ez((T)0.0, (T)0.0, (T)1.0, (T)1.0);
 
    Quaternion<T> qx, qy, qz;
    qz.setRotation(e.element1(), ez);
    qx.setRotation(e.element2(), ex);
    qy.setRotation(e.element3(), ey);
 
    (*this) = qy*qx*qz;
    if (s<(T)0.0) (*this) = - (*this);
}

References Vector< T >::element1(), Vector< T >::element2(), Vector< T >::element3(), and Quaternion< T >::setRotation().

Referenced by jbxl::ExtEulerZXY2Quaternion().

Here is the call graph for this function:

Here is the caller graph for this function:

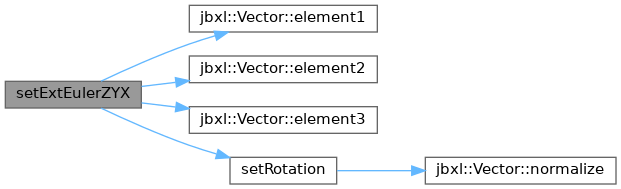
◆ setExtEulerZYX()

template<typename T >

void setExtEulerZYX ( Vector< T > e )

Definition at line 373 of file Rotation.h.

{
    Vector<T> ex((T)1.0, (T)0.0, (T)0.0, (T)1.0);  
    Vector<T> ey((T)0.0, (T)1.0, (T)0.0, (T)1.0);  
    Vector<T> ez((T)0.0, (T)0.0, (T)1.0, (T)1.0);
 
    Quaternion<T> qx, qy, qz;
    qz.setRotation(e.element1(), ez);
    qy.setRotation(e.element2(), ey);
    qx.setRotation(e.element3(), ex);
 
    (*this) = qx*qy*qz;
    if (s<(T)0.0) (*this) = - (*this);
}

References Vector< T >::element1(), Vector< T >::element2(), Vector< T >::element3(), and Quaternion< T >::setRotation().

Referenced by jbxl::ExtEulerZYX2Quaternion().

Here is the call graph for this function:

Here is the caller graph for this function:

◆ setRotate() [1/2]

template<typename T = double>

void setRotate	(	T	e,
		T	X,
		T	Y,
		T	Z,
		T	N = (T)0.0 )

inline

Definition at line 77 of file Rotation.h.

77{ Vector<T> v(X, Y, Z, N); setRotation(e, v);}

◆ setRotate() [2/2]

template<typename T = double>

void setRotate	(	T	e,
		Vector< T >	v )

inline

Definition at line 76 of file Rotation.h.

76{ setRotation(e, v);}

◆ setRotation() [1/2]

template<typename T = double>

void setRotation	(	T	e,
		T	X,
		T	Y,
		T	Z,
		T	N = (T)0.0 )

inline

Definition at line 74 of file Rotation.h.

74{ Vector<T> v(X, Y, Z, N); setRotation(e, v);}

References Quaternion< T >::setRotation().

Referenced by Quaternion< T >::setRotation().

Here is the call graph for this function:

Here is the caller graph for this function:

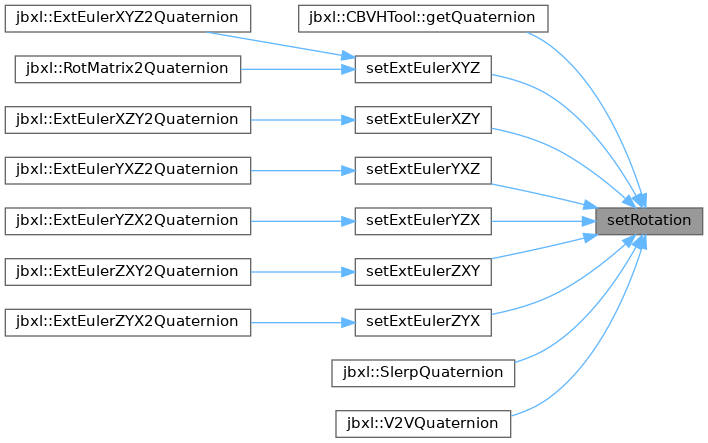
◆ setRotation() [2/2]

template<typename T >

void setRotation	(	T	e,
		Vector< T >	v )

回転を定義する

Parameters

e	回転角．ラジアン単位．
v	回転軸

Definition at line 311 of file Rotation.h.

{
    if (v.n!=(T)1.0) v.normalize();
 
    if (e>(T)PI)       e = e - (T)PI2;
    else if (e<-(T)PI) e = (T)PI2 + e;
 
    T s2 = e/(T)2.0;
    T sn =(T) sin(s2);
    s  = (T)cos(s2);
    x  = v.x*sn;
    y  = v.y*sn;
    z  = v.z*sn;
    n  = (T)v.n;
    c  = (T)1.0;
}